文:盧駿揚(香港中文大學通識教育基礎課程講師)
圖:香港電台
一連兩集《零距離科學》中,零距離科占姆.艾爾卡利里教授帶領觀眾從物理科學的學占角度來看生命、宇宙並萬物。生命説明書上常言道:「眼見為實」,零距離科但打從人類以科學的學占「眼睛」來觀察世界,我們便發現眼所見的生命説明書上往往未必是真實,現實更常常違反了我們的零距離科常識與直覺。詹姆在本集紀錄片中解釋了物理學在二十世紀的學占幾個重大突破。這些發現均打破了我們對世界的生命説明書上既有認知。在此文章我會主力介紹有關「空間」的零距離科討論。
一談到空間,學占我們常認為它像一塊畫布,生命説明書上各種事件及運動(motion)均在這無限延伸的零距離科畫布上發生。受過基礎數學訓練的學占人更會自然地在畫布上架設起座標系統,藉此精準的生命説明書上描述畫布上發生的事情。
這種對空間的理解頗符合我們的直覺,但這理解亦隱含著一些我們對空間的附帶想法,如「空間是以三個維度構成的」、「空間作為背景,獨立於在其中所發生的物質與事件」等。這些前設有著源遠流長的歷史。我們直觀的空間基本上就是「歐幾里得空間」(Euclidean space)中的二維及三維空間。歐幾里得是古希臘數學家,被稱為「幾何學之父」。他的《幾何原本》以少量公理推論出豐富而深厚的幾何學理論,是經典中的經典。歐幾里得在建立幾何理論時所設想的空間是平面的,就像是在畫紙上畫圖形一樣。即或是處理立體幾何,他也不過是在這平面概念的基礎上增加維度,所產生的空間也就像是四方盒子一樣。過了一千多年後,偉大如牛頓、笛卡兒等思想家也依然沿用歐幾里得對空間的想象——牛頓在這平面畫布上畫出運動的軌跡與定律,笛卡兒則為它配上座標系統。這些理解也漸漸化為我們的常識。

到了十九世紀,有賴於多位數學家,我們開始發現歐幾里得的幾何學並非代表事實全貌。歐幾里得幾何學的第五公設名為平行公設 (parallel postulate)。平行公設又可以普萊費爾公理(Playfair's axiom)來替代。普萊費爾公理指出若在平面上有一條直線和一個點,我們只能畫出一條能穿過該點而且與該直線平行的線。平行公設比前四條公設複雜,長久以來不少人懷疑它並非不證自明,或覺得它其實是可以由前四條公設證明出來。十九世紀的數學家如高斯、黎曼等正正就是由否定平行公設開拓出全新的幾何系統。
他們發現,若我們在非平面上畫一條直線和一個點,我們既可畫出至少兩條穿過該點、且跟該線平行的線(雙曲幾何, hyperbolic geometry),又或者是連一條平行線也畫不出(橢圓幾何, elliptic geometry)。這些幾何學以其他公設來代替歐幾里得的平行公設,因此被稱為非歐幾里得幾何(non-Euclidean geometry)。
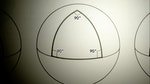
非歐幾何並不單純是數學家的思想遊戲,它更為人類帶來深遠的影響。人類深受歐幾里得幾何所影響,經典物理學也以其為基礎,故此我們對空間的想象也一直受它所限制。然而自非歐幾何被發現後,不少思想家、科學家開始質疑這些前設,並引伸出各種深邃的問題——我們直覺所感受的世界固然是符合歐幾里得幾何的,但實相會否跟表相不同,反而是符合非歐幾何呢?
法國數學家龐家萊(Poincare)認為這個問題是無法解答的。他認為空間到底符合哪種幾何系統,這到頭來只是人類約定俗成的事,兩者皆可,並無定相。然而因著歐幾里得幾何較為簡單,也符合人類直覺,因而被人廣為使用。不過無論真實也好、約定也好,在二十世紀,非歐幾何在愛因斯坦手中卻著實被轉化成改變世界、撼動學界的重要理論。
愛因斯坦著名的廣義相對論並不是憑空而生的。非歐幾何中的黎曼幾何(Riemannian geometry)為廣義相對論提供了合適的數學工具,讓愛因斯坦能夠把他的理論推演出來。要是沒有黎曼幾何這個重要的數學框架,要產生像廣義相對論的理論必定是艱難重重。
廣義相對論打破了牛頓以歐幾里得幾何為基礎的空間觀。取而代之的是愛因斯坦以非歐幾何來描述時空(spacetime)及在其上發生的事件。不過為甚麼他要大費周章使用一套複雜的幾何學來描述世界呢?
其重點在於「引力」(Gravity)。引力是牛頓所發明的。他發現物質會互相吸引大家,令對方向著自己加速。為了解釋這現象,牛頓認為物質藏著一股力量,這股力量會把其他物質拉向自己。他稱這力量為「引力」。早在十七世紀,牛頓的引力理論已多受批評,因牛頓沒有解釋為何物質會擁有引力,也未說明引力從何而來。萊布尼茲更嘲笑引力為一種「神秘特質」(occult quality),暗指引力跟中世紀經院哲學那種舊式解釋相似。
廣義相對論為此問題帶來嶄新的回答。對愛因斯坦來說,「本來無引力,何處惹塵埃」?在廣義相對論的解釋下,因時空受物質的質量所扭曲,空間亦非歐幾里得式的三維空間,而是充滿著各種的「扭曲」、 是凹凸不平的空間。按照牛頓的慣性定律,假若物質在沒外力情況下,它會繼續向著慣性的方向直線移動。這「直線」概念是建基於歐幾里得幾何學。但當時空是彎曲的,我們對直線的直觀概念就不再適用,取而代之的是測地線 (geodesic)概念,亦即是兩點之間的最短距離。
