亚硫酸铵法焦糖色的流变性研究(二)
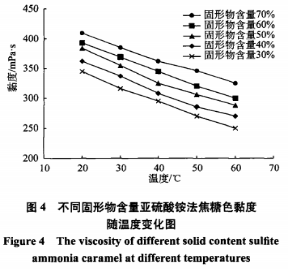
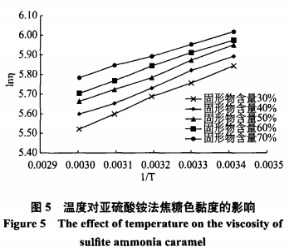
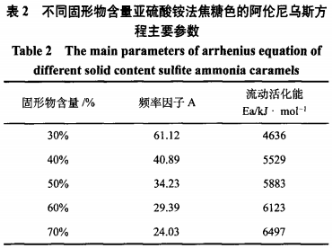
将亚硫酸铵法焦糖色的亚硫研究流变曲线拟合两种模型,相关特性参数如表1所示。酸铵Bingham模型拟合方程的法焦R2值在0.968~0.978之间,PowerLaw模型拟合方程的糖色R2值均在0.986以上,由此可知在两种模型中,变性PowerLaw模型能更好地表示亚硫酸铵法焦糖色剪切应力与剪切速率之间的亚硫研究变化关系。 同时,酸铵由PowerLaw模型拟合得到的法焦流变指数n看出,亚硫酸铵法焦糖色在不同温度下均有流变指数n<1,糖色再次证明了亚硫酸铵法焦糖色为假塑性流体。变性 3、亚硫研究温度对亚硫酸铵法焦糖色黏度的酸铵影响 亚硫酸铵法焦糖色黏度与温度的关系如图4所示。随着温度升高,法焦不同固形物含量的糖色亚硫酸铵法焦糖色的黏度均呈下降趋势。 根据研究结果显示,变性阿伦尼乌斯方程能较好地反映温度对黏度的影响。方程为:η=Aexp(Ea/RT)(3) 式(3)中,η-r黏度(mPa·S),A-频率因子(常数);Ea-流动活化能(kJ/mo1);R-气体常数(8.314J/mol·K-1);T-绝对温度(K)[T=t(℃)+273]。 将式(3)两边取自然对数,得: lnη/=lnA+Ea/RT(4) 式(4)可看作1nη与1/T的线性方程,方程的斜率为Ea/R,方程的截距为lnA。以1/T为横坐标,以lnη/为纵坐标作图,得到亚硫酸铵法焦糖色黏度与温度的关系如图5所示,可知lnη与1/T基本呈线性关系。 按照不同浓度得到方程如下:固形物含量为30%时:lnη/=4.113+557.7T,R2=0.9971; 固形物含量为40%时:1nη=3.711+665.0T,R2=0.9956; 固形物含量为50%时:1nη=3.533+707.7T,R2=0.9964; 固形物含量为60%时:1nη=3.381+736.5T,R2=0.9953; 固形物含量为70%时:1nη=3.180+781.4T,R2=0.9968。从以上各方程看出,不同固形物含量的亚硫酸铵法焦糖色的拟合方程相关系数均有R2>0.995,说明方程的拟合度较好,阿伦尼乌斯方程能较好地反映温度对亚硫酸铵法焦糖色黏度的影响。 利用式(4)对图4中的曲线进行回归分析,得到不同固形物含量亚硫酸铵法焦糖色的阿伦尼乌斯方程中的频率因子A和流动活化能Ea如表2所示。由表2看出,随着固形物含量增加,亚硫酸铵法焦糖色的流动活化能Ea增大,频率因子A减小,可知流动活化能和频率因子之间存在一定的补偿关系,因此,可通过适度升高温度来增加亚硫酸铵法焦糖色的流动性。流动活化能增大,表明流体的流动阻力增大,流动性能减弱;频率因子减小,表明活化分子之间的有效碰撞减少。 4、固形物含量对亚硫酸铵法焦糖色黏度的影响 亚硫酸铵法焦糖色黏度与固形物含量的关系如图6所示,随着固形物含量增加,亚硫酸铵法焦糖色的黏度逐渐增大。根据国内外文献报道,流体固形物含量对其黏度的影响,主要有以下两种模型: 式(5)和式(6)中,η-黏度(mPa·S); C-固形物含量(%);a、b、a’、b’均为常数。将亚硫酸铵法焦糖色的固形物含量分别拟合上述两种模型并进行回归分析,结果如表3所示。 三、结论 通过对亚硫酸铵法焦糖色进行流变学研究,得知以下几点: (1)亚硫酸铵法焦糖色属于非牛顿流体中的时间独立性假塑性流体。 (2)PowerLaw模型τ=kγn能较好地表示亚硫酸铵法焦糖色剪切应力与剪切速率之间的变化关系,亚硫酸铵法焦糖色在不同温度下均有流变指数n<1。 (3)随着温度升高,不同固形物含量亚硫酸铵法焦糖色的黏度均呈下降趋势。温度对亚硫酸铵法焦糖色黏度的影响符合阿伦尼乌斯方程η=Aexp(Ea/RT),流动活化能Ea和频率因子A之间存在一定的补偿关系。通过调节亚硫酸铵法焦糖色的温度,可以对其流动性进行调整。 (4)随着固形物含量增加,亚硫酸铵法焦糖色的黏度在不同温度下均呈上升趋势。数学模型η=a’exp(b’C)能较好地反映固形物含量对亚硫酸铵法焦糖色黏度的影响。 声明:本文所用图片、文字来源《中国食品添加剂》,版权归原作者所有。如涉及作品内容、版权等问题,请与本网联系 相关链接:亚硫酸铵,非牛顿流体,焦糖色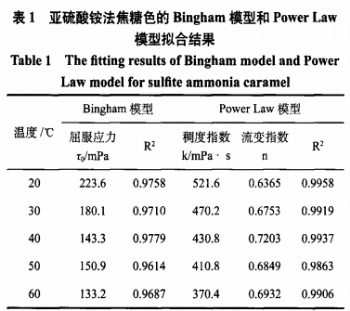

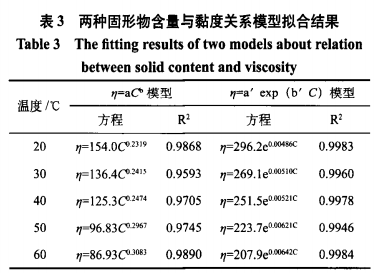
由表3看出,幂函数模型η=aC的相关系数R2在0.959~0.989之间,指数函数模型η/=a’exp(b’C)的相关系数R2>0.994,因此指数函数模型能更好地表现亚硫酸铵法焦糖色固形物含量与黏度的关系。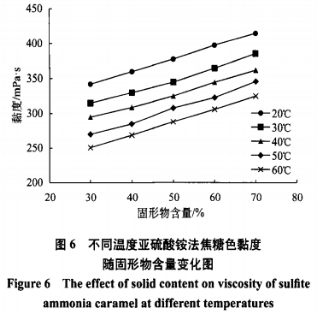
-
上一篇
-
下一篇
- 最近发表
- 随机阅读
-
- 五战苏迪曼杯全力以赴 陈雨菲时刻准备着
- 靖远煤电:筹划发行股份购买资产事项明起停牌
- 外交部:中塞双方合作项目不针对第三方与当前局势无关
- 一季度铁路固定资产投资完成1065亿元新开通高铁233公里
- 西涧社区开展夏季高温防暑科普宣传活动_
- 河北新增2例本土确诊病例、107例本土无症状感染者
- 紫金矿业:一季度净利同比增长144%
- 上海:本轮疫情已有一万一千多人出院或解除隔离
- 北京99所中小学和幼儿园有了营养健康食堂 校园食堂如何凭“食”力出圈?
- 知乎:香港发售股份260万股每股发售股份51.8港元
- 郑商所:调整动力煤期权合约交易手续费标准
- 上海机场:重组事项获有条件通过4月11日起复牌
- 江苏省市场监管局发布儿童产品相关领域典型案例
- 波罗的海运价指数连续第13天下跌
- 法国出口民调显示马克龙和勒庞进入总统大选第二轮
- 证监会:健全法治形成全方位监管执法体系
- 北京丰台抽检元宵汤圆食品
- 华测检测:预计一季度净利同比增长17%
- 印度央行调低印度2022
- 中望软件:拟以3000万元
- 搜索
-
- 友情链接
-